La forme même des pyramides est là pour nous prouver que, dans l'ancienne Égypte aussi, les ouvriers avaient déjà tendance à travailler de moins en moins. Will Cuppy
Pyramides (2500 av. J.-C.)
Pharaon Kheops (2538-2516 av. J.-C.): il fit construire la Grande Pyramide de Gizeh (pyramide de Kheops) qui abrite sa dépouille.
L'une des sept merveilles du monde antique.

Pharaon Khephren (vers 2500 av. J. -C.), successeur de Kheops, il fit construire la deuxième pyramide de Gizeh.
Pharaon Mykerinus: constructeur de la 3e pyramide de Giseh.
Gizeh ou Guizèh, ville sur la rive gauche du Nil, on y trouve ces trois pyramides et le Sphinx.
Les quelques citations et données suivantes sont principalement extraites du livre "Le secret de la Grande Pyramide" de Georges Barbarin.

Plateau de Gizeh et géométrie sacrée

Google Earth en Pyramides de Gizeh
LE SECRET de la GRANDE PYRAMIDE
Dimensions
* Quelques mesures principales de la Pyramide, en chiffres de notre système métrique. Les mesures de l'astronome Piazzi Smith correspondent à :
Base carrée de côté 232, 805 mètres
Hauteur 148, 208 mètres
Quantité de pierres 6 millions
Quantité de couches 200
* Le circuit de base de la Pyramide est de 36 524 pouces, nombre qui correspond cent fois le nombre de jours de l'année.
* Les diagonales de la base font 25 826,5 pouces et la hauteur totale est de 5 813 pouces (axe vertical central).
Orientation
* Aves les premiers astronomes et premiers géomètres du monde, l'orientation de la Grande Pyramide vers les quatre points cardinaux est irréprochable: elle est exacte, à quatre minutes trente-cinq secondes près (autre source: 3' 6).
Le couloir descendant est aligné avec l'étoile polaire.
Pi et la quadrature du cercle
* Aujourd'hui on peut calculer la valeur de Pi avec n'importe quel nombre de décimales, sans jamais trouver la dernière, ce qui démontrerait que la quadrature du cercle est une définitive impossibilité. C'est évidemment la transcendance de Pi (prouvée par Lindemann 1882) qui rend inéluctablement le calcul des décimales de Pi sans fin.
* Avant Jésus-Christ les données oscillaient entre 3 10/70 et 3 10/71.
* Du temps des Pharaons, avait-on une valeur très précise de Pi? Divisons le périmètre de la Pyramide (931,22 m) par deux fois l'axe vertical (148, 208 m x 2):
931,22 / (2 x 148,208) = 3,141598 ...
À comparer à Pi = 3,141592654 ...
Rayon de la Terre
* Constatation du célèbre directeur de l'Observatoire de Bourges: la coudée sacrée, soit 0,635 660 m, multipliée par dix millions, égale 6 356 600 mètres, rayon polaire de la Terre (6 356,8 km).
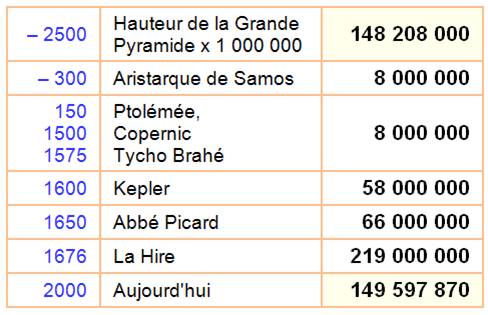
Distance Terre-Soleil - Historique
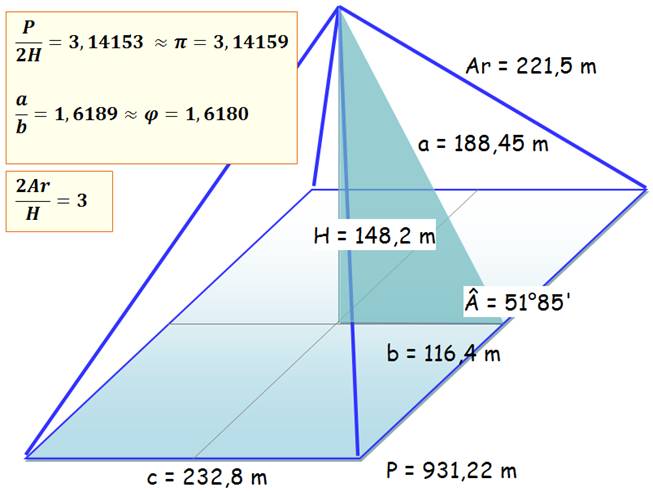
PYRAMIDE de KHEOPS - Dimensions
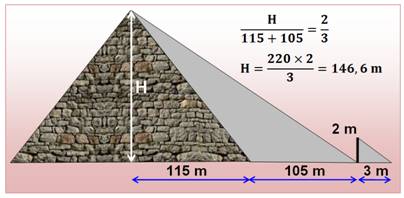
Calcul à la Thalès de Milet
* Thalès est connu pour avoir calculé la hauteur de la grande pyramide de Gizeh. La mesure directe est impossible. Il utilisa la propriété suivante:
Dans deux triangles semblables, triangles qui ont des angles égaux deux à deux, les côtés sont proportionnels.
* La légende dit que Thalès plaça son bâton à la lisière de l'ombre de la pyramide. Il prétend alors que la proportion bâton-ombre est la même pour hauteur-longueur de l'ombre de la pyramide
To calculate the height of the Great Pyramid at Giza, Thales used the following proposition: two similar triangles, triangles with identical angles, have their three sides in proportion.
He knew that his staff (bâton) was 2 m long. All he had to do was measure the length of the shadow of the pyramid and the length of the shadow cast by his staff.
* Le côté de la base carrée de la pyramide mesure 230 m; son bâton fait 2 m de long et projette une ombre de 3m.
* Il mesure l'ombre depuis la base de la pyramide et trouve 105 m.
* En appliquant son principe de proportions, il évalue la hauteur de la pyramide à 146,66m.
Légende ou réalité?
De nombreux sites ou ouvrages relate l'estimation faite par Thales Il existe une interrogation entre deux méthodes possibles:
* mesure via l'ombre portée par la pyramide et un bâton (ratio method), ou
* mesure lorsque l'ombre de la pyramide couvrait exactement une face de la pyramide (equal shadow method).
Il est plus probable qu'il s'agisse du premier cas. Ce qui est certain, c'est que dans le deuxième cas, il faut attendre des conditions propices qui ne se renouvellent pas plus de quatre fois par an.