Vous n'êtes pas identifié.
• Annonce ToutSurTout
Déjà 15 ans !

Si vous souhaitez participer vous aussi aux discussions sur le forum, il faut vous inscrire ou vous identifier.
Les inscriptions sont actuellement OUVERTES.
Message 51 Réponse postée le 27-11-2020 à 16:24:43
El Roslino 






- Titre: VIP
- Avancement: Niveau 5
- Lieu: U.S.A
- Date d'inscription: 07-07-2016
- Messages: 33 217
- Site web
Re: Les radiateurs
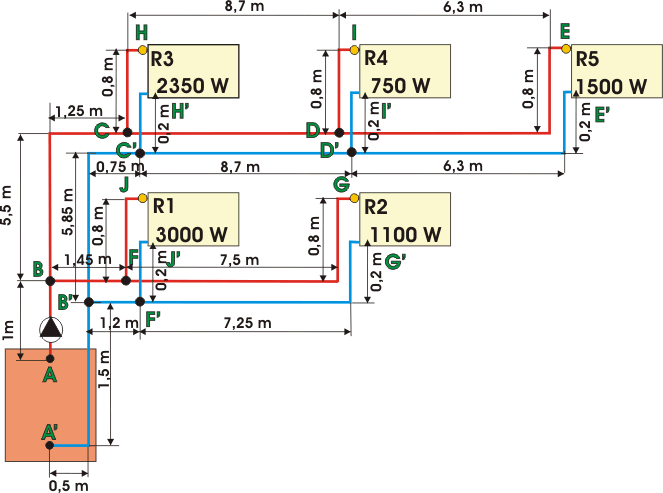
Singularités du tronçon AB/B'A'.
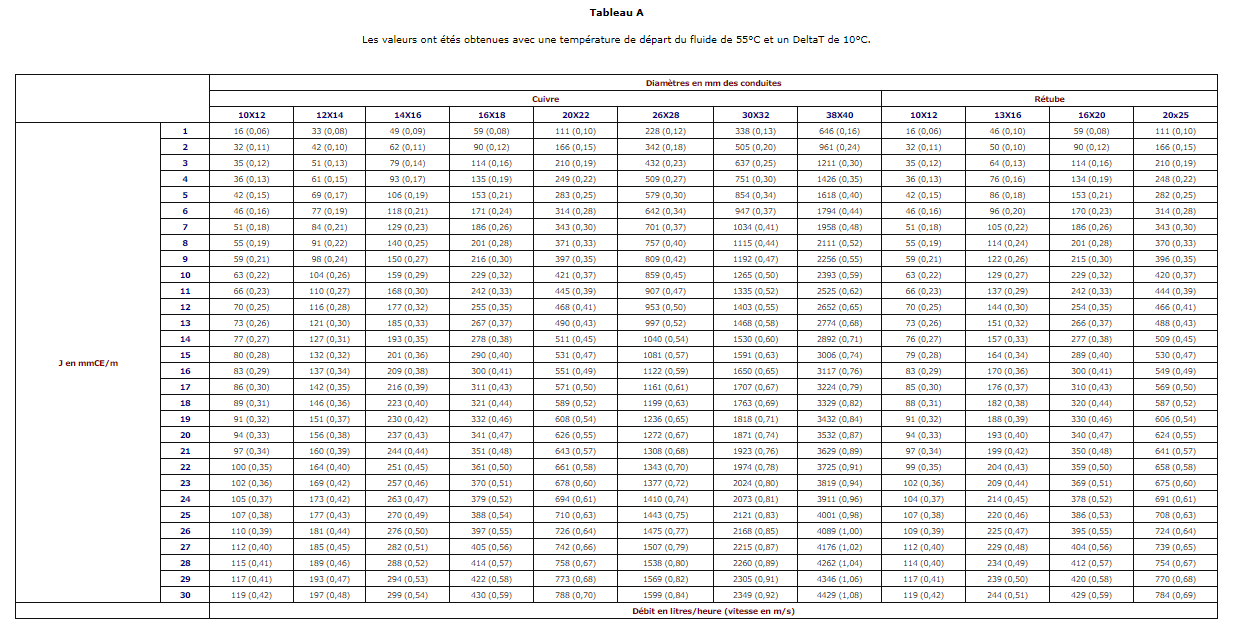
Diamètre 20x22
Vitesse du fluide 0,54 m/s
8 coudes 90° du commerce R 3cm : Cs = 1
4 coudes 45° du commerce R 3cm : Cs = 0,7
2 vannes à boules : Cs = 0,5
1 chaudière : Cs = 5
8 coudes 90° R 3cm : Z = 114,14
4 coudes 45° R 3cm : Z = 39,95
2 vannes : Z = 14,27
1 chaudière : Z = 71,34
Pertes totales : 114,14 + 39,95 + 14,27 + 71,34 = 239,70 mmCE
Z = 239,70 x 1,25 = 299,63
Ici, on va à nouveau rajouter un pourcentage pour prendre en compte les différents raccords de la panoplie comme la soupape différentielle, doigts de gants des thermomètres, etc... On va prendre ici une valeur de 30%.
Donc Z = 299,63 x 1.30 = 389,52
Les pertes de charge singulières totales pour le circuit le plus défavorisé s'élèvent à : 81,16 + 41,97 + 55,51 + 239,70 = 418,34 mmCE

Message 52 Réponse postée le 27-11-2020 à 16:25:21
El Roslino 






- Titre: VIP
- Avancement: Niveau 5
- Lieu: U.S.A
- Date d'inscription: 07-07-2016
- Messages: 33 217
- Site web
Re: Les radiateurs
Pertes de charge totales du circuit le plus défavorisé (J + Z) s'élèvent à :
751,08 + 418,34 = 1169,42 mmCE.
En prenant la HM nominale de la vitesse 1 du circulateur pour le débit de 614 l/h, 1250 mmCE, la perte de charge résultante est de 1250 - 1169,42 = 80,58 mmCE, dans ce cas, le résultat est bon mais il ne faut pas avoir oublié de raccords ou de coudes et bien suivre le cheminement car cette perte résultante est assez mince et une variation des paramètres utilisés pourrait induire une perte de charge plus importante qui pourrait dépasser celle du circulateur et entraîner une sous alimentation du radiateur le plus défavorisé.
Il suffit maintenant de procéder de la même manière pour calculer le reste du circuit. Dans cet exemple, le rapport J/Z est de 64/36% :
J = 751,08 / 1169,42 x 100 = 64,22%
Z = 418,34 / 1169,42 x 100 = 35,77%

Message 53 Réponse postée le 27-11-2020 à 16:25:48
El Roslino 






- Titre: VIP
- Avancement: Niveau 5
- Lieu: U.S.A
- Date d'inscription: 07-07-2016
- Messages: 33 217
- Site web

Message 54 Réponse postée le 27-11-2020 à 16:28:47
El Roslino 






- Titre: VIP
- Avancement: Niveau 5
- Lieu: U.S.A
- Date d'inscription: 07-07-2016
- Messages: 33 217
- Site web
Re: Les radiateurs
Connaître diverses valeurs d'un radiateur.
Les résultats obtenus ici ne seront qu'approximatifs car trop de facteurs rentrent en ligne de compte, comme la précision des appareils de mesure (thermomètres, débitmètre) , les différents DeltaTTm/Ti (voir légende) utilisés par les fabricants pour leurs calculs, 90/70/20 ou 90/75/20 (température du fluide à l'entrée du radiateur / température du fluide à la sortie du radiateur / température de la pièce) donc 60 ou 55°C ceci pour les radiateurs antérieur à 1997 et 75/65/20 donc 50°C pour les radiateurs postérieur à 1997, les différents DeltaTTd/Tr, en général 20 ou 15°C pour les radiateurs antérieur à 1997 et maintenant 10°C alors que la profession utilise toujours.
En général, un DeltaTTd/Tr de 15°C pour éviter les débits trop importants et donc les pertes de charge plus élevées.
Le fait que l'installateur ou l'ingénieur thermicien est ou non surdimensionné le radiateur pour fonctionner à une température de chaudière plus basse et ceci afin de réduire les coûts d'exploitation (ce qu'il est conseillé de faire).
Malgré tout, les résultats suffiront pour avoir une bonne idée de la situation.
Légende :
Td = température de départ (température à l'entrée du radiateur)
Tr = température de retour (température à la sortie du radiateur)
Tm = température moyenne du radiateur Tm = (Td + Tr) / 2
Ti = température de la pièce
Q = puissance en Watts
D = débit en litres/heure
p = masse volumique de l'eau en kg/litre en fonction de sa température (voir tableau à la page "Formules/Tableaux") p doit être pris à la température moyenne du radiateur : (Td + Tr) / 2
c = coefficient de chaleur spécifique de l'eau c = 1,1627
n = exposant de la loi d'émission n = 1,287 (valeur moyenne pour l'extrapolation de puissance à un autre DeltaTTm/Ti )
DeltaTTm-Ti = différence de température entre la température moyenne du fluide et celle de la pièce. Température de la pièce qui doit être prise au centre de celle-ci et à la hauteur de 1,5 m du sol. DeltaTTm-Ti = ((Td + Tr) / 2) - Ti
DeltaTTd-Tr = différence de température du fluide entre l'entrée et la sortie du radiateur DeltaTTd-Tr = Td - Tr
DeltaTTm-Ti_connu = DeltaT (température moyenne du fluide - température de la pièce) connu, sert de base pour connaître la puissance du radiateur à un DeltaTTm/Ti différent (calcul par extrapolation)
DeltaTTm-Ti_désiré = DeltaT (T° moyenne du fluide - T° de la pièce) désiré, sert de but pour connaître la puissance du radiateur à un DeltaTTm/Ti voulu (calcul par extrapolation)

Message 55 Réponse postée le 27-11-2020 à 16:32:01
El Roslino 






- Titre: VIP
- Avancement: Niveau 5
- Lieu: U.S.A
- Date d'inscription: 07-07-2016
- Messages: 33 217
- Site web
Re: Les radiateurs
Connaître le débit d'eau du radiateur.
Il est assez difficile de connaître le débit d'eau dans un radiateur par calcul car il faut partir de la puissance annoncée par le fabricant, seulement elle dépend du DeltaT Td-Tr choisi par celui-ci pour la définir, 10, 15 ou 20°C ainsi que du DeltaT Tm-Ti 60, 55 ou 50°C.
Pour un résultat assez fiable, l'emploi d'un débitmètre est conseillé, sinon, par calcul, voici comment procéder :
Pour avoir le DeltaT Td-Tr, utiliser 2 thermomètres, 1 à l'entrée et 1 à la sortie du radiateur. Ils peuvent être à applique afin d'éviter tout démontage et bricolage de raccordement, seulement la précision ne sera pas vraiment idéale.
Un thermomètre électronique peu aussi être utilisé mais attention à l'émissivité qui peu influencer légèrement la température indiquée.
Comme le fabricant annonce la puissance de son radiateur pour un DeltaT Tm-Ti donné (60, 55 ou 50°C) et qu'il est peu probable que celui au moment des prises de mesures soit identique, il va donc falloir trouver la puissance approximative en fonction du DeltaT Tm-Ti au moment des mesures.
Dans un 1er temps, prendre les températures entrée/sortie du radiateur, trouver le DeltaT Tm-Ti comme indiqué dans la légende, ensuite, trouver la puissance du radiateur à ce DeltaT Tm-Ti par extrapolation en utilisant la formule suivante :
Q = QFabricant x ((DeltaTTm-Ti_désiré / DeltaTTm-Ti_connu)n)
Exemple :
QFabricant = 1700 W
T° de la pièce = 20°C
T° entrée = 66°C
T° sortie = 58°C
DeltaT Tm-Ti_désiré = celui au moment des mesures : ((66 + 58) / 2) - 20 = 42°C
DeltaT Tm-Ti_connu = celui annoncé par le fabricant : 50°C
puissance extrapolée :
Q = 1700 x ((42 / 50)1,287) = 1358,30 W
débit :
D = Q / (DeltaT Td-Tr x c x p)
D = 1358,30 / (8 x 1,1627 x 0,9822) = 148,66 l/h

Message 56 Réponse postée le 27-11-2020 à 16:32:54
El Roslino 






- Titre: VIP
- Avancement: Niveau 5
- Lieu: U.S.A
- Date d'inscription: 07-07-2016
- Messages: 33 217
- Site web
Re: Les radiateurs
Connaître le DeltaT entrée/sortie du radiateur.
Il faut pour ceci, connaître la puissance du radiateur ainsi que son débit. Dans un 1er temps, extrapoler la puissance en fonction du DeltaTTm/Ti actuel et ensuite utiliser la formule suivante :
DeltaT Td-Tr = Q / D / c / p
Exemple avec les valeurs de l'exemple précédent :
Q = 1700 x ((42 / 50)1,287) = 1358,30 W
DeltaT Td-Tr = 1358,30 / 148,66 / 1,1627 / 0,9822 = 8 °C

Message 57 Réponse postée le 27-11-2020 à 16:36:31
El Roslino 






- Titre: VIP
- Avancement: Niveau 5
- Lieu: U.S.A
- Date d'inscription: 07-07-2016
- Messages: 33 217
- Site web
Re: Les radiateurs
Connaître la puissance en Watts d'un radiateur.
Pour connaître la puissance en Watts d'un radiateur, 3 valeurs sont nécessaires :
- Le débit en litres/heure
- La température d'entrée du fluide dans le radiateur (Td)
- La température de sortie du fluide dans le radiateur (Tr)
Pour obtenir ces valeurs, il est possible de "bricoler" un raccordement avec 2 flexibles, 2 thermomètres et un débitmètre ainsi que divers raccords.
Dans un 1er temps, démonter le radiateur et le poser sur 2 cales en bois d'une hauteur à peu près identique à l'espace qu'il y a entre le bas du radiateur et le sol quand il est accroché au mur puis le raccorder à nouveau à ses conduites d'alimentation en faisant attention à la purge de l'air.
Le fait d'utiliser les flexibles, les divers raccords et le débitmètre augmente un peu les pertes de charge et donc réduit le débit, pour compenser, il suffit de rajouter une dizaine de Watts au résultat.
Comme précisé plus haut, Il faut savoir que le résultat sera approximatif car le débitmètre et les thermomètres ont une marge d'erreur. Pour cette raison, éviter de prendre des pièces sous dimensionnées afin le limiter les pertes de charge.
La formule est la suivante :
Q = D x DeltaTTd-Tr x c x p
Exemple :
D = 125 l/h
T° Entrée = 60°C
T° Sortie = 53°C
Q = 125 x 7 x 1,1627 x 0,9852 = 1002,39 W
Pour connaître la puissance éventuelle du radiateur annoncée par le fabricant (puissance qui a peut être défini le choix du radiateur par l'installateur ou l'ingénieur thermicien), il faut extrapoler à partir du DeltaT Tm-Ti au moment des mesures et savoir si le radiateur est assez récent pour avoir un DeltaT Tm-Ti fabricant de 50 °C avec des valeurs prisent de 75/65/20 ce qui donne un DeltaT Td-Tr de 10 °C, ou si il est plutôt ancien et alors avoir un DeltaT Tm-Ti de 60 ou 55 °C avec des valeurs prisent de 90/70/20 ou 90/75/20 ce qui donne un DeltaT Td-Tr de 20 ou 15 °C.
Exemple en reprenant les valeurs de l'exemple précédent :
Température de la pièce = 20°C
Température moyenne du fluide = 56,5°C
Q = 1002,39 Watts
DeltaT Tm-Ti_désiré = celui probable du fabricant avec un radiateur assez récent : 50 °C
DeltaT Tm-Ti_connu = celui au moment des mesures : (60 + 53) / 2 - 20 = 36,5 °C
Qfabricant = Q x ((DeltaTTm-Ti_désiré / DeltaTTm-Ti_connu)n)
Qfabricant = 1002,39 x ((50 / 36,5)1,287) = 1502,93
p = 0,9777 pour une T° moyenne du fluide de 70 °C : (75 + 65) / 2
DeltaT Td-Tr à cette puissance = 1503 / 125 / 1,1627 / 0,9777 = 10,57 °C
Dans ce cas ci, le débit de la pompe est correct et la puissance trouvée assez précise car le DeltaT Td-Tr du fabricant est probablement de 10 °C.
Si le DeltaT Td-Tr avait été plus grand, il est probable que le débit dans le radiateur est été insuffisant. Si le DeltaT Tm-Ti au moment des mesures est différent de celui du fabricant (sûrement inférieur) et que le DeltaT Td-Tr ai une valeur supérieure ou égale à celui utilisé par le fabricant, il est probable que le débit soit insuffisant ou le radiateur sous dimensionné car le DeltaT Td-Tr est proportionnel au DeltaT Tm-Ti.
Exemple :
D = 125 l/h
Température d'entrée = 60 °C
Température de sortie = 50 °C
Q = 125 x 10 x 1,1627 x 0,9857 = 1432,71 W
DeltaT Tm-Ti_désiré = celui probable du fabricant avec un radiateur assez récent : 50 °C
DeltaT Tm-Ti_connu = celui au moment des mesures : (60 + 50) / 2 - 20 = 35 °C
Qfabricant = Q x ((DeltaT Tm-Ti_désiré / DeltaT Tm-Ti_connu)n)
Qfabricant = 1432,71 x ((50 / 35)1,287) = 2267,34 W
p = 0,9777 pour une température moyenne du fluide de 70 °C
DeltaT Td-Tr à cette puissance = 2267,34 / 125 / 1,1627 / 0,9777 = 15,95 °C
Donc 16 °C au lieu de 10 °C. Ce qui fait que la puissance trouvée est faussée car le débit pour celle-ci avec le
DeltaT Td-Tr du fabricant (10°C) devrai être de : 2267,34 / (10 x 1,1627 x 0,9777) = 199 l/h.
Comme le DeltaT Td-Tr au moment des mesures est déjà de 10 °C il est fort probable que le débit soit insuffisant ou que le radiateur soit sous dimensionné car il atteint déjà la puissance maxi du fabricant, mais comme précisé plus haut, il y a trop de facteurs entrant en jeu pour pouvoir être catégorique sur ce point.
Si par exemple, l'installateur ou l'ingénieur thermicien a utilisé un DeltaT Td-Tr de 15°C le résultat est là, par contre, assez bon. C'est pour cela qu'il est toujours difficile de savoir la puissance réellement installée au moment de l'exécution des travaux si on n'est pas en possession d'un minimum de renseignements.

Message 58 Réponse postée le 27-11-2020 à 16:37:01
El Roslino 






- Titre: VIP
- Avancement: Niveau 5
- Lieu: U.S.A
- Date d'inscription: 07-07-2016
- Messages: 33 217
- Site web
Re: Les radiateurs
Connaître la puissance en Watts d'un radiateur.
Pour connaître la puissance en Watts d'un radiateur, 3 valeurs sont nécessaires :
- Le débit en litres/heure
- La température d'entrée du fluide dans le radiateur (Td)
- La température de sortie du fluide dans le radiateur (Tr)
Pour obtenir ces valeurs, il est possible de "bricoler" un raccordement avec 2 flexibles, 2 thermomètres et un débitmètre ainsi que divers raccords.
Dans un 1er temps, démonter le radiateur et le poser sur 2 cales en bois d'une hauteur à peu près identique à l'espace qu'il y a entre le bas du radiateur et le sol quand il est accroché au mur puis le raccorder à nouveau à ses conduites d'alimentation en faisant attention à la purge de l'air.
Le fait d'utiliser les flexibles, les divers raccords et le débitmètre augmente un peu les pertes de charge et donc réduit le débit, pour compenser, il suffit de rajouter une dizaine de Watts au résultat.
Comme précisé plus haut, Il faut savoir que le résultat sera approximatif car le débitmètre et les thermomètres ont une marge d'erreur. Pour cette raison, éviter de prendre des pièces sous dimensionnées afin le limiter les pertes de charge.
La formule est la suivante :
Q = D x DeltaT Td-Tr x c x p
Exemple :
D = 125 l/h
T° Entrée = 60°C
T° Sortie = 53°C
Q = 125 x 7 x 1,1627 x 0,9852 = 1002,39 W
Pour connaître la puissance éventuelle du radiateur annoncée par le fabricant (puissance qui a peut être défini le choix du radiateur par l'installateur ou l'ingénieur thermicien), il faut extrapoler à partir du DeltaT Tm-Ti au moment des mesures et savoir si le radiateur est assez récent pour avoir un DeltaT Tm-Ti fabricant de 50 °C avec des valeurs prisent de 75/65/20 ce qui donne un DeltaT Td-Tr de 10 °C, ou si il est plutôt ancien et alors avoir un DeltaT Tm-Ti de 60 ou 55 °C avec des valeurs prisent de 90/70/20 ou 90/75/20 ce qui donne un DeltaT Td-Tr de 20 ou 15 °C.
Exemple en reprenant les valeurs de l'exemple précédent :
Température de la pièce = 20°C
Température moyenne du fluide = 56,5°C
Q = 1002,39 Watts
DeltaT Tm-Ti_désiré = celui probable du fabricant avec un radiateur assez récent : 50 °C
DeltaT Tm-Ti_connu = celui au moment des mesures : (60 + 53) / 2 - 20 = 36,5 °C
Qfabricant = Q x ((DeltaTTm-Ti_désiré / DeltaTTm-Ti_connu)n)
Qfabricant = 1002,39 x ((50 / 36,5)1,287) = 1502,93
p = 0,9777 pour une T° moyenne du fluide de 70 °C : (75 + 65) / 2
DeltaT Td-Tr à cette puissance = 1503 / 125 / 1,1627 / 0,9777 = 10,57 °C
Dans ce cas ci, le débit de la pompe est correct et la puissance trouvée assez précise car le DeltaT Td-Tr du fabricant est probablement de 10 °C.
Si le DeltaT Td-Tr avait été plus grand, il est probable que le débit dans le radiateur est été insuffisant. Si le DeltaT Tm-Ti au moment des mesures est différent de celui du fabricant (sûrement inférieur) et que le DeltaT Td-Tr ai une valeur supérieure ou égale à celui utilisé par le fabricant, il est probable que le débit soit insuffisant ou le radiateur sous dimensionné car le DeltaT Td-Tr est proportionnel au DeltaT Tm-Ti.
Exemple :
D = 125 l/h
Température d'entrée = 60 °C
Température de sortie = 50 °C
Q = 125 x 10 x 1,1627 x 0,9857 = 1432,71 W
DeltaT Tm-Ti_désiré = celui probable du fabricant avec un radiateur assez récent : 50 °C
DeltaT Tm-Ti_connu = celui au moment des mesures : (60 + 50) / 2 - 20 = 35 °C
Qfabricant = Q x ((DeltaT Tm-Ti_désiré / DeltaT Tm-Ti_connu)n)
Qfabricant = 1432,71 x ((50 / 35)1,287) = 2267,34 W
p = 0,9777 pour une température moyenne du fluide de 70 °C
DeltaT Td-Tr à cette puissance = 2267,34 / 125 / 1,1627 / 0,9777 = 15,95 °C
Donc 16 °C au lieu de 10 °C. Ce qui fait que la puissance trouvée est faussée car le débit pour celle-ci avec le
DeltaT Td-Tr du fabricant (10°C) devrai être de : 2267,34 / (10 x 1,1627 x 0,9777) = 199 l/h.
Comme le DeltaT Td-Tr au moment des mesures est déjà de 10 °C il est fort probable que le débit soit insuffisant ou que le radiateur soit sous dimensionné car il atteint déjà la puissance maxi du fabricant, mais comme précisé plus haut, il y a trop de facteurs entrant en jeu pour pouvoir être catégorique sur ce point.
Si par exemple, l'installateur ou l'ingénieur thermicien a utilisé un DeltaT Td-Tr de 15°C le résultat est là, par contre, assez bon. C'est pour cela qu'il est toujours difficile de savoir la puissance réellement installée au moment de l'exécution des travaux si on n'est pas en possession d'un minimum de renseignements.

Message 59 Réponse postée le 27-11-2020 à 17:09:32
El Roslino 






- Titre: VIP
- Avancement: Niveau 5
- Lieu: U.S.A
- Date d'inscription: 07-07-2016
- Messages: 33 217
- Site web